AR Model in Python
08.08.2021
Intro
The auto regression model, or AR model, predicts a value at a particular time using previous lags (values at previous times). The model relies on the correlations between lags, or auto correlations, since the correlations are based on the same series. In this article, we will learn how to build an Autoregression model in Python.
The Model Math
Let's take a brief look at the mathematical definition. We predicted value of an AR model follow this equation for AR(1)
Where:
- is a constant
- is our coefficient
- is the previous value at time t-1
- is the error of the current time
If we want to expand to Ar(2) and more, we get add another lag, previous time value, and another coefficient. For example.
Let's say we have an AR model and we have the following sales for two months: [300]. We can then predict y_3 for the third month as follows:
Where we find c and phi by performing linear regression on the data set and the e_t is assumed to be sampled from a normal distribution.
Dataset
To test out ARIMA style models, we can use ArmaProcess function. This will simulate a model for us, so that we can test and verify our technique. Let's start with an AR(1) model using the code below. To create an arr model, we set the model params to have order c(1, 0, 0). This order represents 1 AR term, 0 diff terms, and 0 MA terms. We also pass the value of the AR parameter which is .7.
from statsmodels.tsa.arima_process import ArmaProcess
import numpy as np
ar = np.array([1, -.7])
ma = np.array([1])
ar_simulater = ArmaProcess(ar, ma)
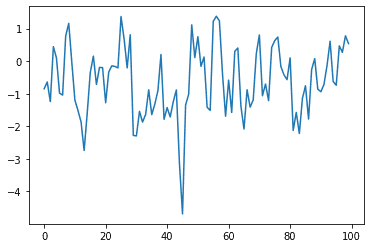
ar_sim = ar_simulater.generate_sample(nsample=100)import matplotlib.pyplot as plt
plt.plot(ar_sim)[<matplotlib.lines.Line2D at 0x2718333e850>]Viewing the ACF or PACF
When trying to model ARMA models, we usually use the ACF or PACF. It is worth noting that before this, you will want to have remove trend and seasonality. We will have a full article on ARIMA modeling later on. For AR models, the PACF will help us determine the component, but we also need to confirm the ACF does not drop off as well.
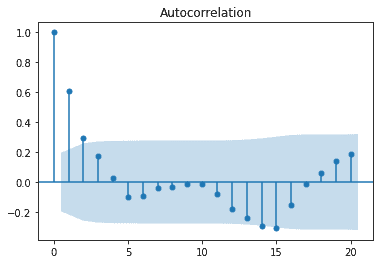
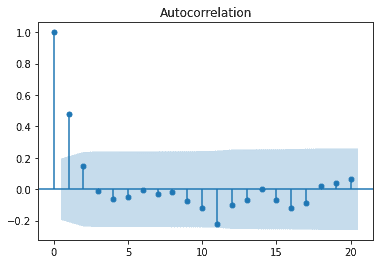
We start with the ACF plot. We can see there is not drastic drop off, there is simply a small degredation over time.
from statsmodels.graphics import tsaplots
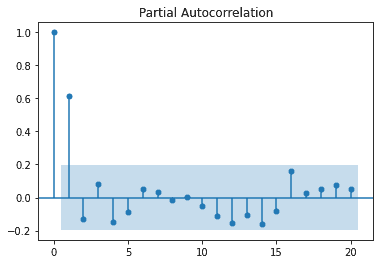
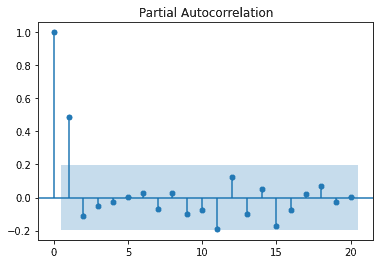
tsaplots.plot_acf(ar_sim)We now look at the PACF plot. We can see a steep drop off after the first lag suggesting an AR(1) model because the data seems highly correlated with the previous lage, value at the previous time. We expect this since we simulated that data.
from statsmodels.graphics import tsaplots
tsaplots.plot_pacf(ar_sim)Fitting the Model
We can use the built in arima function to model our data. We pass in our data set and the order we want to model.
## Ignore some warnings
import warnings
warnings.filterwarnings('ignore')from statsmodels.tsa.arima_model import ARMA
mod = ARMA(ar_sim, order=(1, 0))
res = mod.fit()
res.summary()| Dep. Variable: | y | No. Observations: | 100 |
|---|---|---|---|
| Model: | ARMA(1, 0) | Log Likelihood | -136.537 |
| Method: | css-mle | S.D. of innovations | 0.945 |
| Date: | Sun, 08 Aug 2021 | AIC | 279.074 |
| Time: | 18:44:51 | BIC | 286.890 |
| Sample: | 0 | HQIC | 282.237 |
| coef | std err | z | P>|z| | [0.025 | 0.975] | |
|---|---|---|---|---|---|---|
| const | 0.1478 | 0.253 | 0.584 | 0.559 | -0.348 | 0.644 |
| ar.L1.y | 0.6323 | 0.079 | 7.990 | 0.000 | 0.477 | 0.787 |
| Real | Imaginary | Modulus | Frequency | |
|---|---|---|---|---|
| AR.1 | 1.5816 | +0.0000j | 1.5816 | 0.0000 |
We can see the ar1 was modeled at .68 which is very close to the .7 we simulated. Another value to check here is the aic, 147.11, which we would use to confirm the model compared to others.
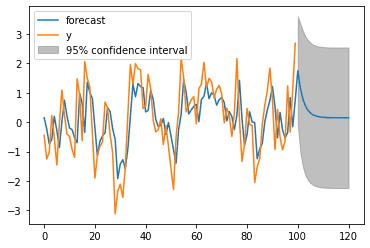
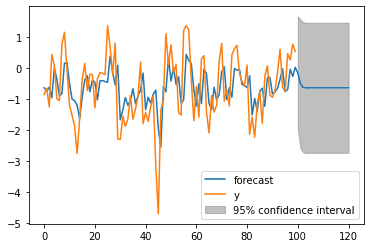
We can now forecast our model using the plot_predict function. Here we predict 20 time values forward and plot the new values.
res.plot_predict(start=0, end = 120)Modeling an AR(2)
Let's finish with one more example. We will go a bit quick, and use all the steps above.
- Get our data
from statsmodels.tsa.arima_process import ArmaProcess
import numpy as np
ar2 = np.array([1, -.7, .4])
ma2 = np.array([1])
ar2_simulater = ArmaProcess(ar2, ma2)
ar2_sim = ar_simulater.generate_sample(nsample=100)import matplotlib.pyplot as plt
plt.plot(ar2_sim)[<matplotlib.lines.Line2D at 0x271838ab820>]- Plot the ACF and PACF
from statsmodels.graphics import tsaplots
tsaplots.plot_acf(ar2_sim)tsaplots.plot_pacf(ar2_sim)- Fit and Predict
from statsmodels.tsa.arima_model import ARMA
mod = ARMA(ar2_sim, order=(2, 0))
res = mod.fit()
res.summary()| Dep. Variable: | y | No. Observations: | 100 |
|---|---|---|---|
| Model: | ARMA(2, 0) | Log Likelihood | -134.941 |
| Method: | css-mle | S.D. of innovations | 0.932 |
| Date: | Sun, 08 Aug 2021 | AIC | 277.883 |
| Time: | 18:45:41 | BIC | 288.303 |
| Sample: | 0 | HQIC | 282.100 |
| coef | std err | z | P>|z| | [0.025 | 0.975] | |
|---|---|---|---|---|---|---|
| const | -0.6301 | 0.162 | -3.878 | 0.000 | -0.949 | -0.312 |
| ar.L1.y | 0.5324 | 0.099 | 5.374 | 0.000 | 0.338 | 0.727 |
| ar.L2.y | -0.1027 | 0.099 | -1.032 | 0.302 | -0.298 | 0.092 |
| Real | Imaginary | Modulus | Frequency | |
|---|---|---|---|---|
| AR.1 | 2.5926 | -1.7371j | 3.1207 | -0.0940 |
| AR.2 | 2.5926 | +1.7371j | 3.1207 | 0.0940 |
res.plot_predict(start=0, end = 120)