How to Conduct a Shapiro Test in R

Intro

When building different models like regression and conduct statistical tests such as ANOVA, t-tests, etc, it is often required that the data be normally distributed. To check for this, you can verify visually and by using a number of tests. The Shapiro-Wilk test is one of those normality tests that is very popular and widely used. In this article, we will learn how to test normality with the Shapiro-Wilk test in R.

The Shapiro Wilk Test

R provides a method called shapiro.test that takes in a vector, which is usually your sample, and conducts the shaprio wilk test on that sample. The function will also provide the W statistic from the shaprio wilk test and a p-value. The default test is based on an alpha of .05. One other thing to note, is that your sample size must be between 3-5000 to use the test.

Using the Shaprio-Wilk Test

Let’s see how the shaipro.test works in action. We will start with an example on data that follows the normal distribution. Do this, we can use the rnorm function to generate a sample of random normal numbers.

sample = rnorm(1000)

shapiro.test(sample)

## 
##  Shapiro-Wilk normality test
## 
## data:  sample
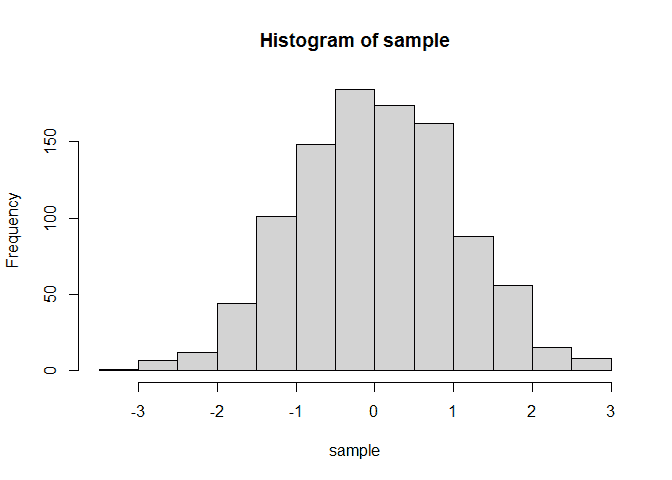
## W = 0.99899, p-value = 0.867

You can also check this visually using a histogram.

hist(sample)

Non-Normal Data

Now that we see how the shaipro.test works on normally distributed data, let’s see the opposite. We can generate a sample for the chi-squared distribution and conduct the same test.

sample = rnorm(1000)

shapiro.test(sample)

## 
##  Shapiro-Wilk normality test
## 
## data:  sample
## W = 0.99847, p-value = 0.534

You can also check this visually using a histogram.

hist(sample)