How to Conduct a Normality Test in R

Intro

Many tests in statics and other tasks rely on the assumption that your data is somewhat normally distributed. For example, when modeling with linear regression, normality is assumed. This is similar for many hypothesis tests. In this article, we will learn how to conduct Normality Tests in R.

Loading the Data

For this tutorial, we will use the mtcars data set that is built in to R. We can load using the following command: data(mtcars).

data(mtcars)
head(mtcars)

##                    mpg cyl disp  hp drat    wt  qsec vs am gear carb
## Mazda RX4         21.0   6  160 110 3.90 2.620 16.46  0  1    4    4
## Mazda RX4 Wag     21.0   6  160 110 3.90 2.875 17.02  0  1    4    4
## Datsun 710        22.8   4  108  93 3.85 2.320 18.61  1  1    4    1
## Hornet 4 Drive    21.4   6  258 110 3.08 3.215 19.44  1  0    3    1
## Hornet Sportabout 18.7   8  360 175 3.15 3.440 17.02  0  0    3    2
## Valiant           18.1   6  225 105 2.76 3.460 20.22  1  0    3    1

Visual Normality Tests

There are two visual tests we can conduct to check normality. The first is to plot the distribution of our variables and see if the distribution matches the normal distribution. Let’s see an example with the horse power of our cars in the mtcars data set. We can see the horse power seems to be skewed right and does not follow the normal distribution.

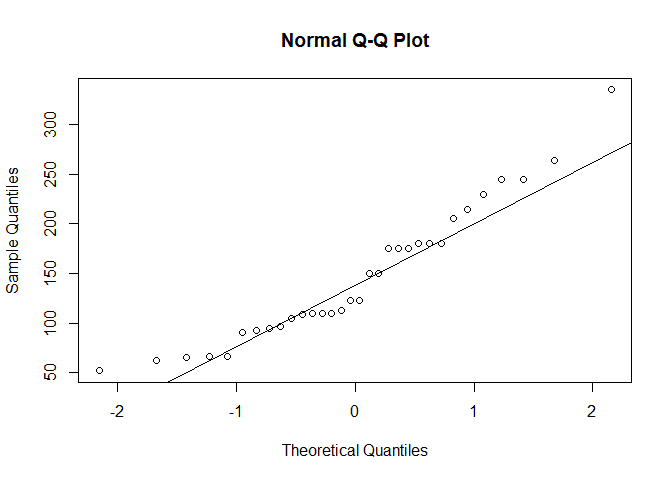
hist(mtcars$hp)

The second way is to create a QQ plot. On a QQ plot we look to see if the data follows a straight, positive, increasing line. We can use R’s qqnorm and qqline to create this plot.

## Plot with a qqnorm and line
qqnorm(mtcars$hp)
qqline(mtcars$hp)

Above we can see that the poitns deviate from the straight line and don’t seem to follow a normal distribution.

Hypothesis Tests

In addition to the visual tests, we can use hypothesis test to check if our data is normally distributed. The Shapiro-Wilk’s normality test is one of the most widely used test. We can run this test using the shapiro.test function in R.

shapiro.test(mtcars$hp)

## 
##  Shapiro-Wilk normality test
## 
## data:  mtcars$hp
## W = 0.93342, p-value = 0.04881

The null hypothesis of the Shapiro-Wilk test is that the data is normal. In our test above, we can get a p-value of .04881 which would be rejected at the .05 level concluding the data is not normal. However, it would not be rejected at the .01 level.