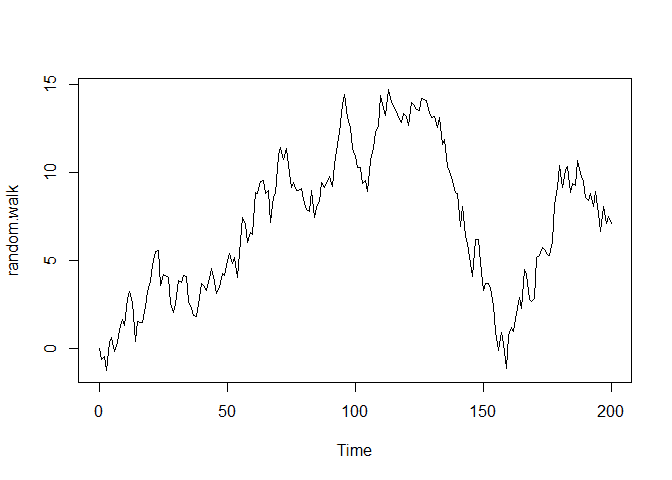Augmented Dickey-Fuller Test in R

Intro

In time series analysis, we often want to check if a time series is stationary. This is because when modeling, most of our techniques rely on stationary time series. One way to check for a stationary seires is to use the Augmented Dicky-Fillter Test. In this article, we will learn how to conduct the Augmented Dickey-Fuller Test in R.

The Augmented Dickey-Fuller Test is a hypothesis test. The null-hypothesis is that the time series is non-stationary, and the alternative is that the series is stationary. Thus, we need to find a p-value low enough to reject our null hypothesis, thus suggesting the series is stationary.

How to Conduct the Augmented Dickey-Fuller Test in R

Let’s first create a random walk of data. We can use the arima.sim method to create a rank walk. By definition, the random walk is non-stationary.

# Set seed so you can reproduce.
set.seed(1)

random.walk <- arima.sim(
  model = list(order = c(0, 1, 0)),
  n = 200
)


plot(random.walk, type='l')

Now, we an perform the dickey-fuller test. Do do this, we will use the adf.test method from the tseries package.

library(tseries)

## Registered S3 method overwritten by 'quantmod':
##   method            from
##   as.zoo.data.frame zoo

adf.test(random.walk)

## 
##  Augmented Dickey-Fuller Test
## 
## data:  random.walk
## Dickey-Fuller = -1.8516, Lag order = 5, p-value = 0.6382
## alternative hypothesis: stationary

We can see that we received a p-value of .6382, thus we fail to reject the null hypothesis and conclude that our time series is non-stationary.

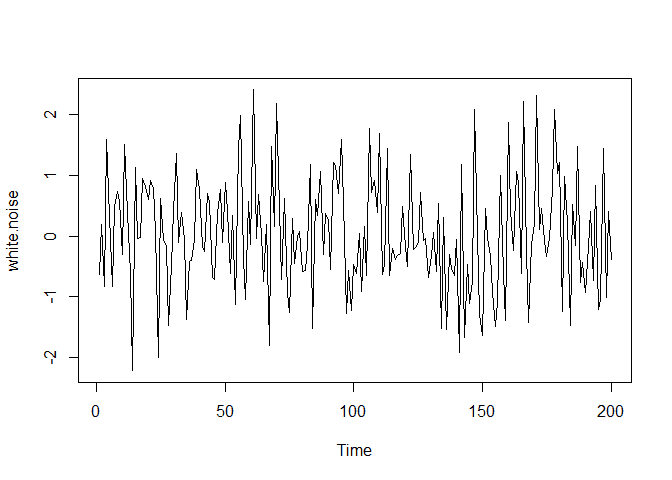
Next. let’s generate a white noise time series, which is by definition stationary.

# Set seed so you can reproduce.
set.seed(1)


white.noise <- arima.sim(
  model = list(order = c(0, 0, 0)),
  n = 200
)

plot(white.noise)

Again, we can use the adf.test method to check for a stationary time series.

library(tseries)

adf.test(white.noise)

## Warning in adf.test(white.noise): p-value smaller than printed p-value

## 
##  Augmented Dickey-Fuller Test
## 
## data:  white.noise
## Dickey-Fuller = -5.737, Lag order = 5, p-value = 0.01
## alternative hypothesis: stationary

Here we receive a p-value of .01 although this might be much smaller and just rounded to 0.01, thus we can reject the null hypothesis as the .05 level (not the .01 level unless this was rounded). This suggest that our time series is stationary. We know this is true since we generated white noise.